Estimated Time: Depending on the students’ previous knowledge of musical notation, the lesson should take about 50-70 minutes.
Summary
Students will watch a segment of the PBS Ken Burns JAZZ documentary about Buddy Bolden creating the “Big Four,” which gave jazz its lilting rhythms as opposed to the straight “boom-chick-boom-chick” of a march. They will then compare and contrast the rhythms of marches and jazz based on the examples in the film, and explore notation, subdivision of notes and the altered and innovative rhythms found in jazz music.
Objectives
- To compare and contrast “straight” march rhythms and jazz rhythms.
- To make explicit connections between musical notation and numerical representation of fractions.
- To notate and perform jazz rhythms.
Materials Needed
- The PBS Ken Burns JAZZ documentary, Episode One “Gumbo.” Begin clip after visual cue heading “The Big Noise,” close up on Buddy Bolden (38:21). Verbal cue: Wynton Marsalis’ voice over picture of Buddy B. saying “Buddy Bolden invented that beat we call the Big Four. End clip after Wynton Marsalis plays Stars and Stripes forever jazz style (40:58).
- CD, tape or recording of a march (preferably “Stars and Stripes Forever” by John Phillip Sousa)
- CD, tape, or recording from the PBS JAZZ Web site of a quick tempo jazz piece
- White board and several colors of dry erase markers, or overhead projector, transparency and several colors of overhead markers
- Computer with Internet access to allow for use of the PBS JAZZ Web site
- Copies of attached worksheets
- Optional: fraction manipulatives in pie pieces and/or bars
Procedures and Activities
Instruct students to stand up and spread out. Lead them through a quick set of stretches (verbally count out eight counts for stretching each of the following body parts: neck, shoulders, torso, arms, legs, and feet).
Tell students that they will be hearing a piece of music and should dance or move accordingly using all of the body parts that they just stretched to reflect the style and feeling of the music. Play a snippet of the march for them. Afterwards, ask them to describe the music and how it made them feel and move, then ask them to identify the type of music it was.
Tell them that they will be hearing a different piece of music and they are to move to this music. Play a snippet of a quick tempo jazz piece and then ask them to describe that piece.
Record their responses on the board in a t-chart like the example shown below:
| March | Jazz |
| Straight | Fun |
| Even | Uneven |
Then watch the video segment from JAZZ Episode One, and add new observations regarding the differences between march rhythm and jazz rhythm.
Next ask them to try and notate the straight march rhythm.
Building on their attempts at notation, show them the correct one and explain how there are 4 beats per measure and each beat is worth 1/4, and that the notes in the straight march rhythm are 1/4 notes (quarter notes). Draw the measure below on the board:

Rewind the video clip again and this time ask them to attempt to notate the “Big Four” rhythm. Rewind the video a few times, but don’t let them dwell on getting it perfect.
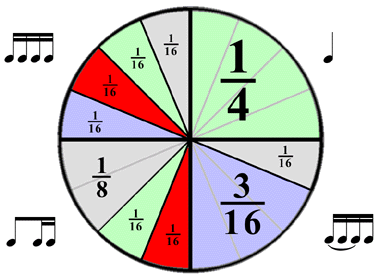
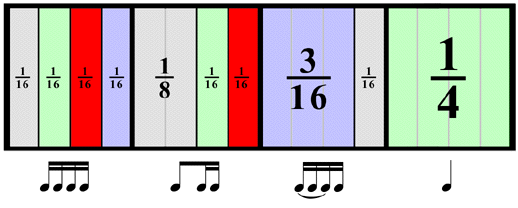
Explain that notes follow the same rules as fractions, hand out the “>Fraction of a Note” chart. To ensure understanding of the chart, pose questions to the group such as:
- How many sixteenths make up 1 quarter note?
- How many quarter notes make up 1 whole note?
- How many sixteenth notes are in two eighth notes?
- How long does a quarter note last?
- How long does an eighth note last?
- How long does a sixteenth note last?
Teach students about subdividing to make the irregular groupings commonly used in jazz rhythms. Show that in 1 beat, you can break it down to four 16th notes, and then you have the option to group those 16th notes in a number of different ways. A particular jazz favorite is the “skipping” or “lilting” rhythm (as termed by Wynton Marsalis in the video) of the dotted 8th-16th note. This involves grouping the first three 16th notes together and leaving the fourth 16th alone (or leaving the first 16th alone and grouping the last three together).
For example:
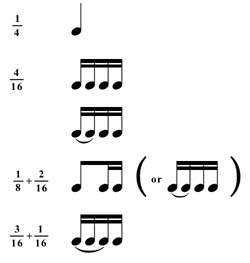
The notation is equivalent to the following two fraction diagrams:
Note that when you group two 16th notes, that it is the same as one 8th note, and that the dot is representing the third 16th note.
Teach how to count out subdivisions. Musicians commonly count 16th notes by using the following syllables:
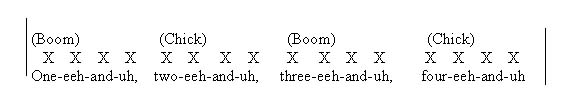
Teach how to clap dotted rhythms by getting a student volunteer to clap straight, even, 16th notes while the teacher models clapping dotted eighth-sixteenth notes. Then assign half of the class to clap 16th notes while the other half claps dotted rhythms.
Now revisit the video clip again and watch and listen to the big four and pick out where the dotted rhythm is.
Show them that by subdividing the beat you can find the dotted rhythm. The first beat is even, in the second beat it gets uneven,

Then show them how the “Big Four” is notated by stringing measures together and subdividing and grouping notes together until it sounds right. (Italicized notes are counted in the musician’s head, but not played.)
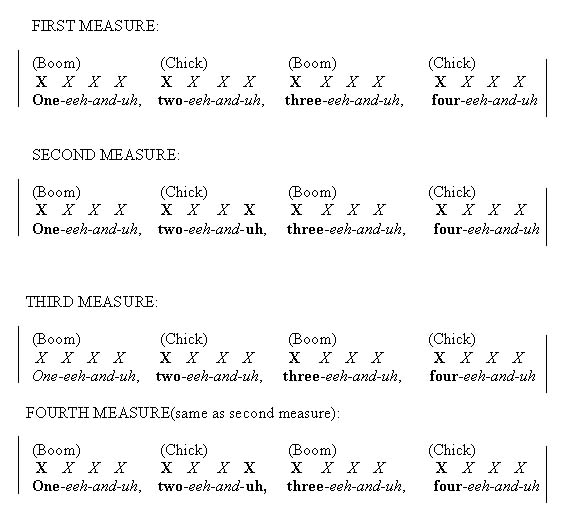
After practicing the rhythms, rewind the video and clap/snap/tap along with Wynton Marsalis on “Stars and Stripes Forever.”
Assessment Suggestions
Students should be able to demonstrate that they know how to subdivide notes and can label or represent the notes with the appropriate fractions. This can be demonstrated by their written performance on an assessment worksheet similar to the ones completed during the lesson and by having individuals clap and count out the rhythms on the assessment sheet.
Extensions / Adaptations
For students who learn better with visuals and hands-on activities, use fraction pie pieces or fraction bar manipulatives to represent the notes. Also, coloring in pictures of fraction bars or pie pieces can be useful.
To help introduce the lesson and activate students’ prior knowledge, one can have students brainstorm lists of words and images that come to mind when thinking about math and words that come to mind when thinking about jazz music. The lists will probably be very different and the lesson can be seen as an attempt to prove that jazz musicians have good brains for math considering all of the innovative counting that they do.
Another opening exercise can involve drawing parallels between “thinking outside the box” and jazz music. After doing the brainteaser, make explicit how jazz musicians have the same notes presented to them but they find new ways of using them. This skill is useful in music, in math, in engineering, in teaching…(the list goes on, elicit some ideas from the class).
Standards
This lesson correlates to the following math and technology standards established by the Mid-continent Regional Educational Laboratory (McREL) at https://www.mcrel.org/:
- Understands how to break a problem into simpler parts or use a similar problem type to solve a problem.
- Formulates a problem, determines information required to solve the problem, chooses methods for obtaining this information, and sets limits for acceptable solutions.
- Generalizes from a pattern of observations made in particular cases, makes conjectures, and provides supporting arguments for these conjectures (i.e., uses inductive reasoning).
- Understands the role of written symbols in representing mathematical ideas and the use of precise language in conjunction with the special symbols of mathematics.
- Uses a variety of strategies (i.e., identify a pattern, use equivalent representations) to understand new mathematical content and to develop more efficient solution methods of problem extensions.
- Understands equivalent forms of basic percents, fractions, and decimals (e.g., 1/2 is equivalent to 50% is equivalent to .5) and when one form of a number might be more useful than another.
- Understands the characteristics and properties (e.g., order relations, relative magnitude, base-ten place values) of the set of rational numbers and its subsets (e.g., whole numbers, fractions, decimals, integers).
- Understands basic number theory concepts (e.g., prime and composite numbers, factors, multiples, odd and even numbers, square
- Uses number theory concepts (e.g., divisibility and remainders, factors, multiples, prime, relatively prime) to solve problems.
- Adds, subtracts, multiplies, and divides whole numbers, fractions, decimals, integers, and rational numbers.
- Uses proportional reasoning to solve mathematical and real-world problems (e.g., involving equivalent fractions, equal ratios, constant rate of change, proportions, percents).
- Understands that mathematics is the study of any pattern or relationship, but natural science is the study of those patterns that are relevant to the observable world.
- Understands that theories in mathematics are greatly influenced by practical issues; real-world problems sometimes result in new mathematical theories and pure mathematical theories sometimes have highly practical applications.
- Understands that new mathematics continues to be invented even today, along with new connections between various components of mathematics.
- Understands that mathematics provides a precise system to describe objects, events, and relationships and to construct logical arguments.
- Understands that mathematicians commonly operate by choosing an interesting set of rules and then playing according to those rules; the only limit to those rules is that they should not contradict each other.
About the Author
Amy Lein has taught mathematics and the performing arts for the past 5 years—but usually not at the same time! Being an advocate for involving all of our multiple intelligences in education, she jumped at the chance to develop lessons linking jazz music to mathematics. Currently she is teaching math and science to high school students with special needs, and continues to play classical violin and sing jazz in her free time.
